题目
Given K sorted linked lists of size N each, merge them and print the sorted output.
Example:
1
2
3
4
5
6
7
| Input: k = 3, n = 4
list1 = 1->3->5->7
list2 = 2->4->6->8
list3 = 0->9->10->11
Output:
0->1->2->3->4->5->6->7->8->9->10->11
|
理解
此题目还有很多种变种,如不固定每个list的长度。不管如何变化,其算法都是一样,选择固定长度的题目,主要是方便时间复杂度的计算
解决
Compare one by one
步骤:
- 创建空链表
- 比较每个list的head元素,取出最小元素,并移动此list的head元素
- 把取出的最小元素链接到空链表里
代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
class Solution {
public int compare(ListNode[] lists){
int minIndex = -1;
for(int i=0; i<lists.length; i++){
if(lists[i] == null) {
continue;
}
if(minIndex == -1 || lists[i].val < lists[minIndex].val){
minIndex = i;
}
}
return minIndex;
}
public ListNode mergeKLists(ListNode[] lists) {
ListNode output = new ListNode(0);
ListNode outputEnd = output;
while(true){
int index = compare(lists);
if(index == -1) {
return output.next;
}
outputEnd.next = lists[index];
outputEnd = lists[index];
lists[index] = lists[index].next;
}
}
}
|
复杂度:
- 时间复杂度:
- 第一层while循环的次数为: K*N 次
- compare()里的for循环次数 K 次
- 时间复杂度为:O(K*N*K)
- 空间复杂度:O(1)
最小堆
通过最小堆优化上面的compare()函数,在写代码之前,我们需要了解最小堆的一些特性:
- 堆可以用数组来表示
- 下标从0开始编号,位置i的元素有如下特性:
- 其parent(i) = (i-1)/2;
- left_child(i) = 2*i + 1;
- right_child(i) = 2*i + 2;
- 修改顶点元素后,恢复其堆的特性的时间复杂度为:O(logK)
代码如下所示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
class Solution {
public int getLeft(int i) {
return 2 * i + 1;
}
public int getRight(int i){
return 2 * i + 2;
}
public void minHeapify(ListNode[] minHeap, int i){
int size = minHeap.length;
while(true){
int min = i;
int left = getLeft(i);
int right = getRight(i);
if(left < size && minHeap[left] != null &&
(minHeap[min] == null || minHeap[min].val > minHeap[left].val)) {
min = left;
}
if(right < size && minHeap[right] != null &&
(minHeap[min] == null || minHeap[min].val > minHeap[right].val)){
min = right;
}
if(min == i) {
break;
}
ListNode temp = minHeap[i];
minHeap[i] = minHeap[min];
minHeap[min] = temp;
i = min;
}
}
public ListNode[] initMinHeap(ListNode[] lists){
ListNode[] minHeap = lists;
int size = minHeap.length;
for(int i=(size-1)/2; i>=0; i--){
minHeapify(lists, i);
}
return minHeap;
}
public ListNode getMin(ListNode[] minHeap){
return minHeap[0];
}
public void replaceMin(ListNode[] minHeap, ListNode node){
minHeap[0] = node;
minHeapify(minHeap, 0);
}
public ListNode mergeKLists(ListNode[] lists) {
if(lists.length == 0){
return null;
}
ListNode output = new ListNode(0);
ListNode outputEnd = output;
ListNode[] minHeap = initMinHeap(lists);
while(true){
ListNode minNode = getMin(minHeap);
if(minNode == null) {
return output.next;
}
outputEnd.next = minNode;
outputEnd = minNode;
replaceMin(minHeap, minNode.next);
}
}
}
|
复杂度:
- 时间复杂度:O(K*N*logK)
- 空间复杂度:O(K)
Divide And Conquer(分治法)
此算法的思路:
- 两两分组合并,形成一个新的数组
- 再重复步骤1,直到只剩一个元素
如下所示:
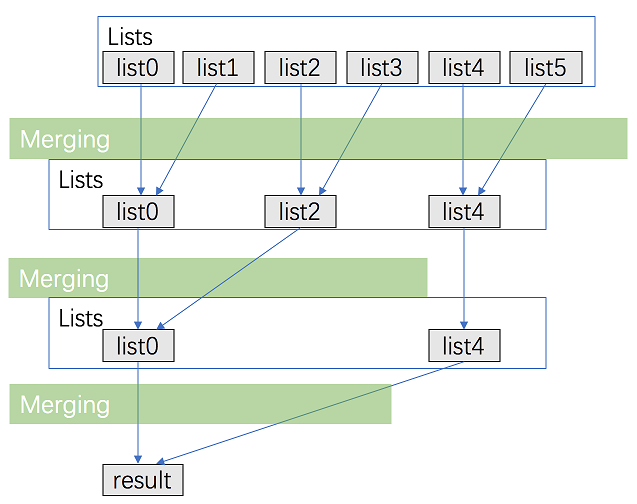
代码省略…
关键来思考其时间复杂度的计算方法:
- Merging的次数为:logK
- listi, listj合并的时间复杂度为0(n)
- 总时间复杂度为=(K/2)*O(N)+(K/2^2)*O(N)+…+(K/2^logK)*O(N)
- 假定(K/2^i)*O(N) 约等于 O(K*N)
- 总时间复杂度约等于O(K*N*logK)

