动态规划

关键点：

1. 动态规划理解：
   1. 适用场景：通过组合子问题的解来求解原问题，同时子问题有重叠的情况。— 如递归函数
   2. 思路：内存换时间，先求解子问题的解并保存，减少重复计算
   3. 注意：动态规划求解的值是最优的，但最优解的路径不唯一，可能有多条
2. 动态规划的步骤：
   1. 计算出状态转移方程，递归地定义最优解的值 —- 如递归函数
   2. 自底向上的方法计算，并保存计算结果
   3. 保存最优解的计算路径 — 使用链表记录
3. 分治法与动态规划的区别：都是通过组合子问题的解来求解原问题，但动态规划会把子问题的解保存下来，减少重复计算，内存与速度的选择。
4. 时间复杂度：通过状态转移方程，可以构建一个棵树，树的很多结点是重复的，分治法的时间复杂度与结点有关，动态规划的时间复杂度与深度有关
5. 递归函数的非递归实现：动态规划
6. KV键值对的存储方案：
   1. 散列表：HashMap
   2. 二叉搜索树（红黑树）：当散列结果不佳时，比HashMap更节省内存

贪心算法

关键点：

1. 定义：动态规划主要减少了子问题重复计算问题，但所有子问题都被计算一次，对于有些问题，可以进步提升性能，如每次计算局部最优，以此局最优的选择推导出全局最优，这样就不用整体计算所有的子问题，这种算法称为贪心算法
2. 步骤：与动态规划类似
   1. 计算出状态转移方程，递归地定义最优解的值 —- 如递归函数
   2. 自顶向下求解，先选择当前最优化的解，再去计算剩余的最优子问题 —- 动态规划是自底向上的方法计算，并保存计算结果
   3. 计算出状态转移方程，递归地定义最优解的值 —— 与动态规划一样
   4. 选择一个贪心选择，并证明贪选择总是安全的（此过程是自顶向下，不依赖子问题的解）
   5. 使用递归算法实现贪心策略
   6. 再使用动态规划的思路，先计算子问题，并保存，实现迭代算法
3. 使用贪心算法求解的问题，总有一个更繁琐的动态规划算法，其区别：
   1. 贪心算法：自顶向下求解，先选择当前最优化的解，再去计算剩余的最优子问题
   2. 动态规则：自底向上，先把最小的子问题求解，再利用子问题求解，需要求解所有的子问题

例子

活动选择问题

问题简单描述：

1. 活动集合：S = {a1, a2, …, an}，使用同一个教室
2. 每个活动ai，都有一个开始时间si和结束时间fi
3. 两个活动[si, fi), [sj, fj]不重叠，表示兼容
4. 问题：选择最大的兼容活动集？

贪心算法的过程

1. 状态转移方程：
   1. c[i, j]：表示活动ai,…,aj的最大兼容活动集
   2. i <= k <=j, 假定最大兼容活动集里必定包含活动ak
   3. c[i, j] = max(c[i, k] + c[k, j] + 1)
2. 贪心策略：结束时间最早的活动一定属于最大的兼容活动集中，证明过程简述：
   1. S = {a1, a2, …., an}，最大兼容活动子集为Ak = {aj, aj+1, …}，且aj是Ak中结束最早的活动，am是S中结束时间最早的活动
   2. 因为 am的结束时间 < aj的结束时间，因此 A’k = {am, aj+1, …}也是S中最大兼容子集
   3. 注意：此证明过程，仅仅只是说明包含最早结束活动的集合是其中一个最优解，但并不是唯一的唯
3. 递归函数：
   1. S = {ai, …, aj} 按结束时间排序，由小到大
   2. c[i, j] = 1 + c[k, j] // ak的开始时间第一个大于ai的结束时间的活动

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

// 递归算法
/**
* int[] s: 表示所有的开始时间
* int[] f: 表示所有的结束时间
* int k: 表示子集的开始
* int n: 表示子集的结束
* List<Integer> maxList: 用于记录最大子集的集合
*/
void recursiveActivitySelector(int[] s, int[] f, int k, int n, List<Integer> maxList) {
    // 子集中{ak, ..., an}中ak的结束时间最小
    maxList.add(k);
    
    // 找到第一个sm > fk的下标m
    m = k + 1;
    while(m <= n && s[m] < f[k]){
        m++;
    }
    recursiveActivitySelector(s, f, m, n, maxList);
}
// 注意：已经按结束时间排序
int[] s; // 开始时间数组
int[] f; // 结束时间数组
recursiveActivitySelector(s, f, 0, s.length - 1);

// 迭代算法
List<Integer> greedyActivitySelector(int[] s, int[] f){
    int n = s.length - 1;
    List<Integer> maxList = new ArrayList<Integer>();
    
    maxList.add(0);
    k = 0;
    for(int m=1; m<=n; m++){
        if(s[m] >= f[k]){
            maxList.add(m);
            k = m;
        }
    }
    return maxList;
}

0-1背包问题

问题描述： 一个正在抢劫商店的小偷发现了n个商品，第i个商品价值vi美元，重wi磅，vi和wi都是整数。这个小偷希望拿走价值尽量高的商品，但他的背包最多能容纳W磅重的商品，W是一个整数。他应该拿哪些物品？

分析：

1. 状态转移方程：
   1. m(i, W)：表示从前i个物品中，选择重量不超过W的物品的最大价值
   2. 每个物品，有选择与不选择两个决策，进而转化为子问题
      
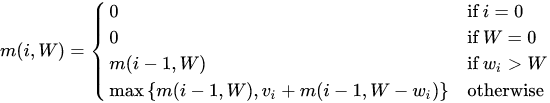
2. 此问题无法使用贪心算法实现，只能使用动态规划求解

分数背包问题

问题描述：与上述的0-1背包问题类似，但对于每个商品，小偷可以拿走其一部分，而不是做（0-1）选择。

分析：此问题就可以使用贪心算法实现，计算每个物品的价值，依次选择价值最高的物品，直到重量达到W

赫夫曼编码（Huffman Code）

问题描述：如何对数据进行压缩

思路：

1. 通过变长的编码实现压缩，实现减少整体字节数，如下所示：
   
2. 由于连字符，为了实现唯一解码结果，不能随意使用变长编码，满足要求的变长编码方式：前缀码
   1. 前缀码：没有任何字符是其他字符的前缀，即每次定位唯一的编码，不会出现多种解码结果

赫夫曼编码：就是使用贪心算法求解的最优前缀码，其大概过程：

1. 初始队列：按频率由低到高
2. 合并最左边两个元素，权重相加构建新元素
3. 按新元素的权重重新排序
4. 重复2，3过程
5. 得到最终的赫夫曼二叉树后，左边路径编码为0，右边的路径编译为1
6. 得到字符的编码，即赫夫曼编码

详情请参考：详细图解哈夫曼Huffman编码树

参考

1. 算法导论
2. 详细图解哈夫曼Huffman编码树