
B-树和B+树学习笔记
B-树
关键点:
- B-树的读法:读做B树,而不是B减树
- 背景:
- 磁盘操作(如数据库),数据库索引是存储在磁盘上的,当数据量比较大时:
- 索引非常大,可能有几个G甚至更多,无法全部加载到内存,只能逐一加载磁盘页
- 磁盘页存储的数据是固定的,对应索引树的节点,即搜索树的节点数据是受磁盘页的大小决定
- 由于磁盘的IO操作比内部的数据比较更加耗时,减少磁盘的IO操作次数是提升定位索引的关键
- 二叉搜索树虽然其查找次数为lgn,但其磁盘的IO操作也是lgn,并不是最优的,需要更加‘矮胖’的数据结构:B-树
- 磁盘操作(如数据库),数据库索引是存储在磁盘上的,当数据量比较大时:
- 定义:B-树是多路平衡查找树,每个节点最多包含m个孩子,m被称为B-树的阶,m的大小由磁盘页的大小决定,m阶的B-树的特征:
- 若根结点不是终端结点,则至少有2棵子树
- 内部结点包含k-1个元素和k个孩子,其中m/2 <= k <= m,即M阶的B-树,内部节点最多含有m-1个元素,最多含有m个孩子,同时至少要有m/2个孩子
- 所有的叶子节点处于同一层
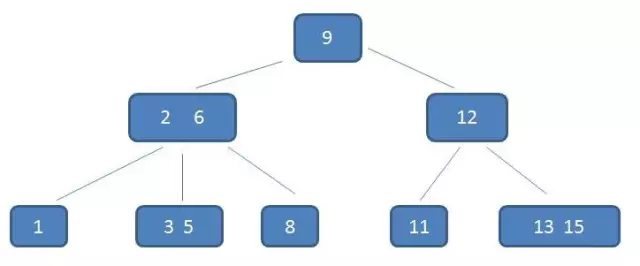
- 操作:
- 查找:与二叉搜索树的查找过程类似
- 删除与添加:如果破坏了B-树的特征,就要进行节点的拆分来恢复特征
- 3阶的添加操作:
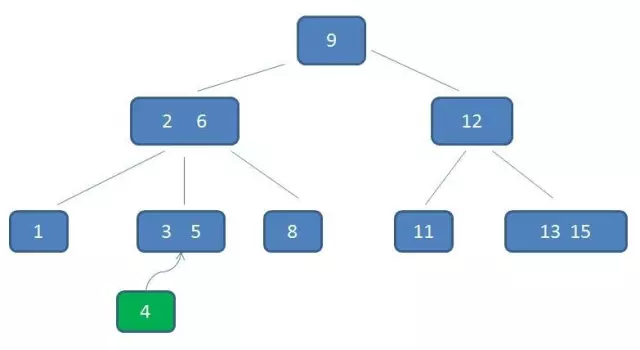
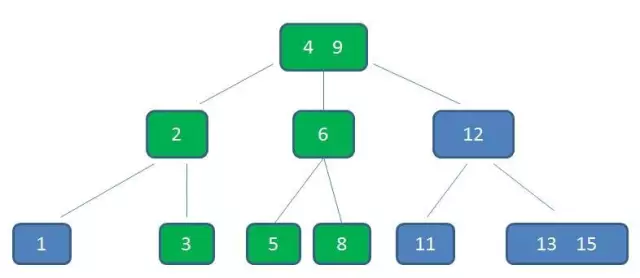
- 3阶的删除操作:
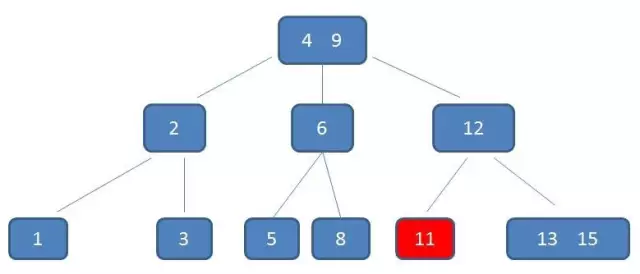
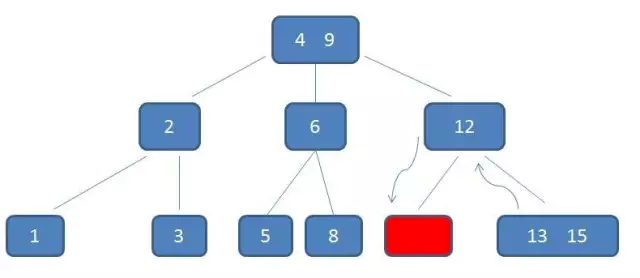
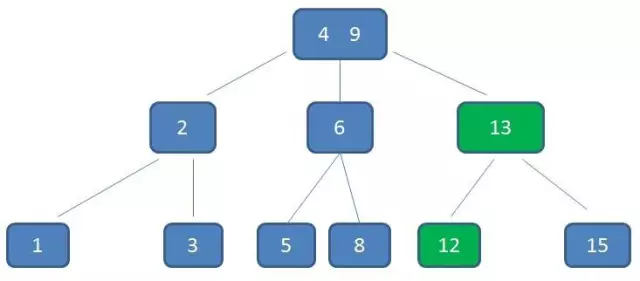
- 3阶的添加操作:
- 应用场景:
- B-树:非关系型数据库的索引实现,如MongoDB
- B+树:关系型数据库的索引实现,如Mysql
B+树
关键点:
- M阶B+树的特征:
- 内部节点有k个元素(B-树有k-1个元素),同时有k个孩子,内部节点不保存索引
- 所有叶子节点包含所有的元素信息(包括内部节点的元素),同时包含所有的索引,关键字自小而大顺序链接
- 如3阶的B+树:
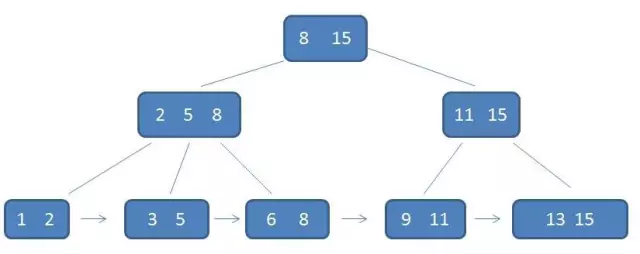
- 比较B-树的优势:
- 内部节点存储更多的元素,使得查询的IO次数更少。
- 所有查询都要查找到叶子节点,查询性能稳定
- 所有叶子节点形成有序链表,便于范围查询,B-树要进行中序遍历才行